wiki, real numbers (http://en.wikipedia.org/wiki/Real_number), wiki, IEEE 854 floating point representation (http://en.wikipedia.org/wiki/IEEE_854), wiki, floating point (http://en.wikipedia.org/wiki/Floating_point). IEEE 754 Converter (http://www.h-schmidt.net/FloatApplet/IEEE754.html) a java applet to convert floating point numbers to 32 bit IEEE 754 representation.

The Python docs on floating point Floating Point Arithmetic (see http://docs.python.org/tut/node16.html).

A compiler writer's view of floating point Lahey Floating Point (http://www.lahey.com/float.htm).

The reasoning behind the IEEE-754 spec: What Every Computer Scientist Should Know About Floating-Point Arithmetic, by David Goldberg, published in the March, 1991 issue of Computing Surveys. Copyright 1991, Association for Computing Machinery, Inc. The paper is available at ACM portal (http://portal.acm.org/citation.cfm?id=103163).

Scientists and engineers are big users of computing and do calculations on non integer numbers (e.g. 0.12). These numbers are called "real" to differentiate them from "imaginary" (now called "complex") numbers. Real numbers measure values that change continuously (smoothly) e.g. temperature, pressure, altitude, length, speed.

	Note
	You will never have to reproduce any of the following information in normal coding, since all the routines have been written for you, but you will have to understand the limitations of floating point representation, or get nonsense or invalid results.

One possible representation of real numbers is fixed point e.g., where the decimal point is in its usual position. Fixed point isn't useful for small or large numbers in fixed width fields (e.g. 8 columns wide) as significant digits can be lost. A small number like 0.000000000008 will be represented at 0.000000 and 123456789.0 will be represented as (possibly) 12345678 or 456789.0. So floating point notation is used. Here's some floating point numbers and their 8-column representation

real                fixed point    floating point
123456789.0         12345678       1.2345E8  (ie 1.2345*10^8)
0.0000000012345678  0.000000       1.234E-9  (ie 1.2345*10-9)

A decimal example of a floating point number is +1.203*10². There is one digit before the decimal point which has a value from 1-9 (the base here being 10). Subsequent digits after the decimal point are divided by 10,100... etc. The term 1.023 is called the mantissa, while the term 2 is called the exponent. A mantissa and exponent are the two components of scientific notation for real numbers. Here's how we calculate the decimal value of +1.203E2

sign     + positive
mantissa 1.203 = 1/1 + 2/10 + 0/100 + 3/1000
exponent 10^2 = 100
+1.203*10^2 = +120.3

Most computers use 64, 80 or 128-bit floating point numbers (32-bit is rarely used for optimisation calculations, because of its limited precision, see floating point precision). Due to the finite number of digits used, the computer representation of real numbers as floating point numbers is only an approximation. We'll explore the reason for this and the consequences here.

One of the early problems with computers was how to represent floating point numbers. Hardware manufacturers all used different schemes (which they touted as a "marketing advantage"), whose main effect was to make it difficult to move numbers between machines (unless you did it in ASCII, or did it between hardware from the same manufacturer). The purpose of these non-standard schemes was to lock the customer into buying hardware from the same manufacturer, when it came time to upgrade equipment.

You'd think that manufacturers would at least get it right, but these different schemes all gave different answers. A C.S. professor in the early days of programmable calculators (1970's) would stuff his jacket pockets with calculators and go around manufacturers and show them their calculators giving different answers. He'd say "what answer do you want?" and give it to them. Eventually a standard evolved (IEEE 854 and 754) which guaranteed the same result on any machine and allowed transfer of numbers between machines in standard format (without intermediate conversion to ASCII).

Hop over to IEEE_854 (http://en.wikipedia.org/wiki/IEEE_854) and look at the bar diagrams of 32- and 64-bit representation of real numbers.

Worked examples on 32- or 64-bit numbers take a while and because of the large number of digits involved, the results aren't always clear. Instead I'll make up a similar scheme for 8-bit reals and work through examples of 8-bit floating point numbers. If we were working on an 8-bit (rather than 32- or 64-bit) computer, here's what an 8-bit floating point number might look like.

Sseemmmm
S    = sign of the mantissa (ie the sign of the whole number)
see  = exponent (the first bit is the sign bit for the exponent)
mmmm = mantissa

Here's a binary example using this scheme.

00101010
Sseemmmm
S      = 0: +ve
see    = 010: s = 0, +ve sign. exponent = +10 binary = 2. multiply mantissa by 2^2 = 4 decimal
mmmm   = 1010: = 1.010 binary = 1/1 + 0/2 + 1/4 + 0/8 = 1.25 decimal
number = + 1.25 * 2^2 = +5.00

Here's another example

11011101
Sseemmmm
S      = 1: -ve number
see    = 101: s = 1, -ve sign. exponent = -01 binary = -1 decimal. multiply mantissa by 2^-1 = 0.5 decimal
mmmm   = 1101: = 1.101 binary = 1/1 + 1/2 + 0/4 + 1/8 = 1.625 decimal
number = - 1.625 * 2^-1 = -0.8125

Doing the same problem with bc -l

11011101
Sseemmmm
#sign is -ve

#checking that I can do the mantissa
# echo "obase=10; ibase=2; 1.101 " | bc -l
1.625

#checking that I can do the exponent. "see" is 101 so exponent is -01
# echo "obase=10; ibase=2; (10)^(-01)" | bc -l
0.5

#the whole number
# echo "obase=10; ibase=2; -1.101 * (10)^(-01)" | bc -l
-0.8125

How many floating point numbers is it possible to represent using a byte (you don't know the value of these numbers or their distribution in the continuum, but you do know how many there are) ^[113] ? (How many reals can you represent using 32-bits ^[114] ?) We could choose any 8-bit scheme we want (e.g. seemmmmm, seeeemmm, mmeeeees, mmmmseee...), but we will still be subject to the 8-bit limit (we will likely have different reals in each set).

In the the seeemmmm scheme used here, where do the numbers come from? The first bit (the sign) has 2 possibilities, we have 3 bits of exponent giving 8 exponents, and 4 bits of mantissa giving us 16 mantissas. Thus we have 2*8*16=256 8-bit floating point numbers.

	Note
	End Lesson 17

Student Example: What real number is represented by the 8-bit floating point number 01101001 ^[115] ? Use bc to convert this number to decimal ^[116]

You aren't allowed to have 0 as the first number of the mantissa. If you get a starting 0 in a decimal number, you move the decimal point till you get a single digit 1-9 before the decimal point (this format is also called "scientific notation"). The process of moving the decimal point is called normalisation.

0.1234*10^3 non-normalised floating point number
1.234*10^2  normalised floating point number.

Is 12.34*10¹ normalised ^[117] ?

Let's see what happens if we don't normalise 8-bit reals. For the moment, we'll ignore -ve numbers (represented by the first bit of the floating point number). Here are the 8 possible exponents and 16 possible mantissas, giving us 8*16=128 +ve numbers.

   eee   E
   000   2^0  =1
   001   2^1  =2
   010   2^2  =4
   011   2^3  =8
   100   2^-0 =1
   101   2^-1 =1/2
   110   2^-2 =1/4
   111   2^-3 =1/8

   mmmm   M
   0000   0
   0001  1/8
   0010  1/4
   0011  3/8
   0100  1/2
   0101  5/8
   0110  3/4
   0111  7/8
   1000  1
   1001  1 + 1/8
   1010  1 + 1/4
   1011  1 + 3/8
   1100  1 + 1/2
   1101  1 + 5/8
   1110  1 + 3/4
   1111  1 + 7/8

Because we have mantissas <1.0, there are multiple representations of numbers, e.g. the number 1/4 can be represented by (1/8)*2 or (1/4)*1; 1 + 1/4 can be represented by (5/8)*2 or 1 + 1/4. We want a scheme that has only one representation for any number. Find other numbers that can be represent in multiple ways - twice ^[118] - trice ^[119] - four times ^[120] - five times ^[121] .

Normalisation says that the single digit before the decimal point can't be 0; we have to start the number with any of the other digits. For decimal the other digits are 1..9. In binary we only have one choice: "any of the other digits" is only 1. All binary floating point numbers then must have a mantissa starting with 1 and only binary numbers from 1.0 to 1.11111.... (decimal 1.0 to 1.99999...) are possible in the mantissa.

Since there's no choice for the value of the first position in the mantissa, real world implementations of floating point representations do not store the leading 1. The algorithm, which reads the floating point format, when it decodes the stored number, knows to add an extra "1" at the beginning of the mantissa. This allows the storage of another bit of information (doubling the number of reals that can be represented), this extra bit is part of the algorithm and not stored in the number.

Here are all the possible normalised mantissas in our 8-bit scheme (the leading 1 in the mantissa is not stored). How many different mantissas are possible in our scheme ^[122] ?

stored				binary		decimal
shortened	true		value		value
mantissa	mantissa	mantissa	mantissa
0000		10000		1.0000		1
0001		10001		1.0001		1 + 1/16 
.
.
1111		11111		1.1111		1 + 15/16

Here's a table of the +ve 8-bit normalised real numbers. (How many +ve 8-bit real numbers are there ^[123] ?) There are only 112 numbers in this list. The 16 entries with see=000 are missing: these are sacrificed to represent 0.0 - we'll explain this shortly - see the non-existance of 0.0. Since a byte can represent an int just as easily as it can represent a real, the table includes the value of the byte, as if it were representing an int.

In my home-made 8-bit real number, the exponent is a signed int. For clarity I've separated out the sign bit of the exponent. If you use the signed int convention, then the first bit of an integer is the sign, with 1 being -ve and 0 being +ve. Remember that if you're using the signed int representation, and you have a 3 bit int, then 000-1=fff.

S see mmmm	int 	M	E	real
0 001 0000	16	1.0	2.0	2.0
0 001 0001	17	1.0625	2.0	2.125
0 001 0010	18	1.125	2.0	2.25
0 001 0011	19	1.1875	2.0	2.375
0 001 0100	20	1.25	2.0	2.5
0 001 0101	21	1.3125	2.0	2.625
0 001 0110	22	1.3750	2.0	2.75
0 001 0111	23	1.4375	2.0	2.875
0 001 1000	24	1.5	2.0	3.0
0 001 1001	25	1.5625	2.0	3.125
0 001 1010	26	1.625	2.0	3.25
0 001 1011	27	1.6875	2.0	3.375
0 001 1100	28	1.75	2.0	3.5
0 001 1101	29	1.8125	2.0	3.625
0 001 1110	30	1.875	2.0	3.750
0 001 1111	31	1.9375	2.0	3.875
0 010 0000	32	1.0	4.0	4.0
0 010 0001	33	1.0625	4.0	4.25
0 010 0010	34	1.125	4.0	4.5
0 010 0011	35	1.1875	4.0	4.75
0 010 0100	36	1.25	4.0	5.0
0 010 0101	37	1.3125	4.0	5.25
0 010 0110	38	1.375	4.0	5.5
0 010 0111	39	1.4375	4.0	5.75
0 010 1000	40	1.5	4.0	6.0
0 010 1001	41	1.5625	4.0	6.25
0 010 1010	42	1.625	4.0	6.5
0 010 1011	43	1.6875	4.0	6.75
0 010 1100	44	1.75	4.0	7.0
0 010 1101	45	1.8125	4.0	7.25
0 010 1110	46	1.875	4.0	7.5
0 010 1111	47	1.9375	4.0	7.750
0 011 0000	48	1.0	8.0	8.0
0 011 0001	49	1.0625	8.0	8.5
0 011 0010	50	1.125	8.0	9.0
0 011 0011	51	1.1875	8.0	9.5
0 011 0100	52	1.25	8.0	10.0
0 011 0101	53	1.3125	8.0	10.5
0 011 0110	54	1.375	8.0	11.0
0 011 0111	55	1.4375	8.0	11.5
0 011 1000	56	1.5	8.0	12.0
0 011 1001	57	1.5625	8.0	12.5
0 011 1010	58	1.625	8.0	13.0
0 011 1011	59	1.6875	8.0	13.5
0 011 1100	60	1.75	8.0	14.0
0 011 1101	61	1.8125	8.0	14.5
0 011 1110	62	1.875	8.0	15.0
0 011 1111	63	1.9375	8.0	15.5
0 100 0000	64	1.0	1.0	1.0
0 100 0001	65	1.0625	1.0	1.0625
0 100 0010	66	1.125	1.0	1.125
0 100 0011	67	1.1875	1.0	1.1875
0 100 0100	68	1.25	1.0	1.25
0 100 0101	69	1.3125	1.0	1.3125
0 100 0110	70	1.375	1.0	1.375
0 100 0111	71	1.4375	1.0	1.4375
0 100 1000	72	1.5	1.0	1.5
0 100 1001	73	1.5625	1.0	1.5625
0 100 1010	74	1.625	1.0	1.625
0 100 1011	75	1.6875	1.0	1.6875
0 100 1100	76	1.75	1.0	1.750
0 100 1101	77	1.8125	1.0	1.8125
0 100 1110	78	1.875	1.0	1.875
0 100 1111	79	1.9375	1.0	1.9375
0 101 0000	80	1.0	0.5	0.5
0 101 0001	81	1.0625	0.5	0.53125
0 101 0010	82	1.125	0.5	0.5625
0 101 0011	83	1.1875	0.5	0.59375
0 101 0100	84	1.25	0.5	0.625
0 101 0101	85	1.3125	0.5	0.65625
0 101 0110	86	1.375	0.5	0.6875
0 101 0111	87	1.4375	0.5	0.71875
0 101 1000	88	1.5	0.5	0.750
0 101 1001	89	1.5625	0.5	0.78125
0 101 1010	90	1.625	0.5	0.8125
0 101 1011	91	1.6875	0.5	0.84375
0 101 1100	92	1.75	0.5	0.875
0 101 1101	93	1.8125	0.5	0.90625
0 101 1110	94	1.875	0.5	0.9375
0 101 1111	95	1.9375	0.5	0.96875
0 110 0000	96	1.0	0.25	0.25
0 110 0001	97	1.0625	0.25	0.265625
0 110 0010	98	1.125	0.25	0.28125
0 110 0011	99	1.1875	0.25	0.296875
0 110 0100	100	1.25	0.25	0.3125
0 110 0101	101	1.3125	0.25	0.328125
0 110 0110	102	1.375	0.25	0.34375
0 110 0111	103	1.4375	0.25	0.359375
0 110 1000	104	1.5	0.25	0.375
0 110 1001	105	1.5625	0.25	0.390625
0 110 1010	106	1.625	0.25	0.40625
0 110 1011	107	1.6875	0.25	0.421875
0 110 1100	108	1.75	0.25	0.4375
0 110 1101	109	1.8125	0.25	0.453125
0 110 1110	110	1.875	0.25	0.46875
0 110 1111	111	1.9375	0.25	0.484375
0 111 0000	112	1.0	0.125	0.125
0 111 0001	113	1.0625	0.125	0.132812
0 111 0010	114	1.125	0.125	0.140625
0 111 0011	115	1.1875	0.125	0.148438
0 111 0100	116	1.25	0.125	0.15625
0 111 0101	117	1.3125	0.125	0.164062
0 111 0110	118	1.375	0.125	0.171875
0 111 0111	119	1.4375	0.125	0.179688
0 111 1000	120	1.5	0.125	0.1875
0 111 1001	121	1.5625	0.125	0.195312
0 111 1010	122	1.625	0.125	0.203125
0 111 1011	123	1.6875	0.125	0.210938
0 111 1100	124	1.75	0.125	0.21875
0 111 1101	125	1.8125	0.125	0.226562
0 111 1110	126	1.875	0.125	0.234375
0 111 1111	127	1.9375	0.125	0.242188

a couple of things to notice

reals have this format:

fixed number of evenly spaced numbers from 1..2 multiplied by 2<superscript>integer_exponent</superscript>.

In the 8-bit scheme here, there are 16 evenly numbers in each 2:1 range. In the range 1..2 the interval is (2-1)/16=1/16=0.0625; the numbers then are 1, 1 + 1/16.. 1 + 15/16. For the range 2..4, you multiply the base set of numbers by 2. There are still 16 evenly spaced intervals and the resulting spacing is (4-2)/16 = 1/8 = 0.125.

In our scheme, how many 8-bit reals are there between 8..16 and what is the interval ^[125] ? How many numbers are there between 0.25..0.5 and what is interval ^[126] ?

Here's a graphical form of the chart of 128 real numbers above. To show the numbers as a 2-D plot

Only the +ve numbers are shown. The first 16 of the possible 128 +ve numbers are not plotted (these are sacrificed to represent the 0.0 and a few other numbers, see the non-existance of 0.0). The absence of these 16 numbers is seen as the gap on the left side, where there are no red dots between 0 and the smallest number on the x-axis.

Note

This is about not being able to read your own code 6 months after you write it: I wrote this section (on floating point numbers) about 6 months before I delivered it in class. (I initially expected I would use it in primitive data types, but deferred it in the interest in getting on with programming.) On rereading, the explanation for the gap on the left hand side, made no sense at all. I couldn't even figure out the origin of the gap from my notes. After a couple of weekends of thinking about it, I put in a new explanation, and then a week later I figured out my original explanation. It was true, but not relevant to the content.

Figure 1. graph of the 7 rightmost bits in a floating point number represented as an integer (X axis) and real (Y axis)

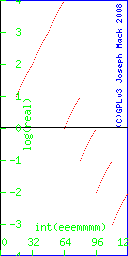The plot is a set of dots (rather than a line or set of lines), showing that you can only represent some of the real space; a few points on the infinity of points that is a line.

	Note
	End Lesson 18

The representation of the +ve reals is

1..2 * 2^exponent.

The 8-bit real numbers (from 0.25 to 4.0) on a straight line look like this (because of crowding, reals<0.25 aren't represented)

Figure 2. graph of the 8-bit real numbers from 0.25..4 plotted on a linear real number line.

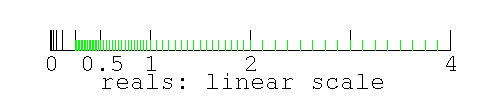There are 16 evenly spaced 8-bit real numbers in any 2:1 section of the real number line (e.g. from 0.25..0.50, 0.50..1.0, 1.0..2.0, 2.0..4.0). Because the length of each segment decreases by half each step going leftward (towards 0.0), the real numbers never get to 0.0 (0.0 would be 2^-∞).

Logarithms:

If you don't know about logarithms

Logarithms are the exponents when reals are represented as base^exponent.

Logarithms do for multiplication, what linear plots do for arithmetic.

Let's say you want a graph or plot to show the whole range of 8-bit reals from 0.125=2^-3 to 16=2⁴. On a linear plot most of the points would be scrunched up at the left end of the line (as happens above). If instead you converted each number to 2^x and plotted x, then the line would extend from -3 to +4, with all points being clearly separated.

If n=2^x, then x is log₂(n). So log₂(1)=0, log₂(2)=1, log₂(4)=2.

If n=2^0.5, then n²=2^0.5*2^0.5=2. Then n=sqrt(2) and 2^0.5 is sqrt(2).

If you multiply two numbers, you add their logarithms.

Logarithms commonly use base 10 (science and engineering; the log of 100 is 2), base 2 (for computing), and log_e (for mathematics, e=2.718281828459)

The 8-bit real numbers (from 0.25 to 4.0) on a logarithmic line look like this

Figure 3. graph of the 8-bit real numbers from 0.25..4 plotted on a log real number line.

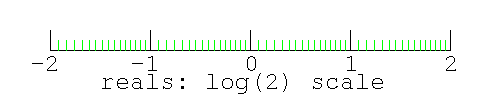Note there are 16 logarithmically spaced real numbers in any 2:1 section of the real number line (e.g. from log₂(number) =-2..-1, -1..0, 0..1, 1..2. Because 0.0 is 2^-∞, 0.0 on this graph is off the left end of the line (at -∞).

How many real numbers can be represented by a 32 bit number ^[127] ? How many floating point numbers exist in the range covered by 32-bit reals ^[128] ?

You can make real numbers as big as you have bits to represent them and as small as you have bits to represent them. However you can't represent 0.0 on the simple floating point scheme shown here.

However 0.0 is a useful real number. Time starts at 0.0; the displacement of a bar from it's equilibrium position is 0.0.

In the above images/graphs, there is no way to represent 0.0 - it's not part of the scheme. Since a normalised decimal number starts with 1..9 and normalised binary numbers start with 1, how do you represent 0.0? You can't. You need some ad hoc'ery (Ad hoc. http://www.wikipedia.org/wiki/Ad_hoc).

To represent 0.0, you have to make an exception like "all numbers must start with 1-9₁₀ or 1₂, unless it's 0.0, in which case it starts with 0". Designers of rational systems are dismayed when they need ad hoc rules to make their scheme work. ad hoc rules indicate that maybe the scheme isn't quite as good as they'd hoped. Exceptions slow down the computer, as rather than starting calculating straight away, the computer first has to look up a set of exceptions (using a conditional statement) and figure out which execution path to follow.

How do we represent 0.0? Notice that the bits for the exponent in the previous section can be 100 or 000; both represent 1 (2⁰ or 2^-0). 8 of our exponents are duplicates. We could handle the duplication, by having the algorithm add 1 to the exponent if it starts with 1, giving us an extra 8 numbers (numbers that are smaller by a factor of 2). However since we don't yet have the number 0.0 anywhere, the convention (in this case of a 1 byte floating point number) is to have two of the 8 numbers with the exponent bits=000 as +/- 0.0. As well we need to represent +/-∞ and NaN, so we use some of the remaining 6 numbers for those.

S  see  mmmm 
0  000  0000 +0.0
1  000  0000 -0.0 (yes there is -0.0)
0  111  0000 +infinity
1  111  0000 -infinity
*  111 !0000 NaN

NaN (not a number): In the IEEE-754 scheme, infinities and NaN are needed to handle overflow and division by 0. Before the IEEE-754 standard, there was no representation in real number space for ∞ or the result of division by zero or over/underflow. Any operation which produced these results had to be trapped by the operating system and the program would be forced to exit. Often these results came about because the algorithm was exploring a domain of the problem for which there was no solution, with division by zero only indicating that the algorithm needed to explore elsewhere. A user would quite reasonably be greatly aggrieved if their program, which had been running happily for a week, suddenly exited with an irrecoverable error, when all that had happened was that the algorithm had wandered into an area of the problem where their were no solutions. The IEEE-754 scheme allows the results of all real number operations to be represented in real number space, so all math operations produce a valid number (even if it is NaN or ∞) and the algorithm can continue. Flags are set showing whether the result came about through over/underflow or division by 0, allowing code to be written to let the algorithm recover.

NaN is also used when you must record a number, but have no data or the data is invalid: a machine may be down for service or it may not be working. You can't record 0.0 as this would indicate that you received a valid data point of 0.0. Invalid or absent data is a regular occurence in the real world (unfortunately) and must be handled. You process the NaN value along with all the other valid data; NaN behaves like a number with all arithmetic operations (+-*/; the result of any operation with NaN always being NaN). On a graph, you plot NaN as a blank.

The number -0.0: is needed for consistency. It's all explained in "What every computer scientist should know about floating-point arithmetic" (link above). It's simplest to pretend you never heard of -0.0. Just in case you want to find out how -0.0 works...

>>> 0.0 * -1
-0.0
>>> -0.0 * 1
-0.0
>>> -0.0 * -1
0.0
>>> -(+0.0)
-0.0		#required by IEEE754
>>> -(+0)		
0		#might have expected this to be -0
>>> -0.0 + 0.0
0.0
>>> -0.0 - 0.0
-0.0
>>> -0.0 + -0.0
-0.0
>>> -0.0 - +0.0
-0.0
>>> -0.0 - -0.0
0.0
>>> 0.0 + -0.0
0.0
>>> 0.0 - +0.0
0.0
>>> 0.0 - -0.0
0.0
>>> i=-0.0
>>> if (i<0.0):
...     print "true"
... 
>>> if (i>0.0):
...     print "true"
... 
>>> if (i==0.0):
...     print "true"
... 
true		#(0.0==-0.0) is true in python
>>> if (i==-0.0):
...     print "true"
... 
true
>>> if (repr(i)=="0.0"):
...     print "true"
... 
>>> if (repr(i)=="-0.0"):
...     print "true"
... 
true

The result of the test (0.0==-0.0) is not defined in most languages. (As you will find out shortly, you can't compare reals, due to the limited precision of real numbers. You can't do it even for reals that have the exact value 0.0).

How many numbers are sacrificed in the 8bit float point representation used here, and in a 32 bit floating point representation (23bit mantissa, 8 bit exponent, 1 bit sign) to allow representation of 0.0, ∞ and NaN ^[129] ? What fraction of the numbers is sacrificed in each case ^[130] ?

	Note
	(with suggestions from the Python Tutorial: representation error).

We've found that only a limited number of real numbers (256 in the case of 8-bit reals, 4G in the case of 32-bit reals) can be represented in a computer. There's another problem: most (almost all) of the reals that have finite representation in decimal (e.g.0.2, 0.6) don't have a finite representation in binary.

Only numbers that evenly divide (i.e. no remainder) powers of the base number (10decimal) can be represented by a finite number of digits in the decimal system. The numbers which evenly divide 10 are 2 and 5. Any number represented by (1/2)ⁿ*(1/5)^m can be represented by a finite number of digits. Any multiple of these numbers can also be represented by a finite number of digits.

In decimal notation, fractions like 1/10, 3/5, 7/20 have finite represenations

1/10=0.1
3/5=0.6
7/20=0.35

In decimal notation, fractions like 1/3, 1/7, 1/11 can't be represented by a finite number of digits.

1/3=0.33333....
1/7=0.14285714285714285714...

Do these (decimal) fractions have finite representations as decimal numbers: 1/20, 1/43, 1/50 ^[131] ?

Here's some numbers with finite represenation in decimal.

#(1/2)^3
1/8=0.125

#3/(2^3)
3/8=0.375

#note 1/80 is the same as 1/8 right shifted by one place. Do you know why?
#1/((2^4)*5)
1/80=0.0125

#1/(2*(5^2))
1/50=0.02

#7/(2*(5^2))
7/50=0.14

Using the above information, give 1/800 in decimal ^[132]

Divisors which are multiples of other primes (i.e. not 2,5) cannot be represented by a finite number of decimals. Any multiples of these numbers also cannot be represented by a finite number of digits. Here's some numbers which don't have finite represenation in decimal.

#1/(3^2)
1/9=0.11111111111111111111...

#1/(3*5)
1/15=0.06666666666666666666...

#4/(3*5)
4/15=0.26666666666666666666...

(the Sexagesimal (base 60) http://en.wikipedia.org/wiki/Sexagesimal numbering system, from the Sumerians of 2000BC, has 3 primes as factors: 2,3,5 and has a finite representation of more numbers than does the decimal or binary system. We use base 60 for hours and minutes and can have a half, third, quarter, fifth, sixth, tenth, twelfth, fifteenth, twentieth... of an hour.)

In binary, only (1/2)ⁿ can be represented by a finite number of digits. Fractions like 1/10 can't be prepresented by a finite number of digits in binary: there is no common divider between 10 (or 5) and 2.

# echo "scale=10;obase=2;ibase=10; 1/10" | bc -l
.0001100110011001100110011001100110

In the binary system, the only number that evenly divides the base (2), is 2. All other divisors (and that's a lot of them) will have to be represented by an infinite series.

Here's some finite binary numbers:

echo "obase=2;ibase=10;1/2" | bc -l
.1
echo "obase=2;ibase=10;3/2" | bc -l
1.1

#3/8 is the same as 3/2, except that it's right shifted by two places.
echo "obase=2;ibase=10;3/8" | bc -l
.011

From the above information give the binary representation of 3/32 ^[133]

Knowing the binary representation of decimal 5, give the binary representation of 5/8 ^[134]

Here's some numbers that don't have a finite represenation in binary

"obase=2;ibase=10;1/5" | bc -l
.0011001100110011001100110011001100110011001100110011001100110011001

#note 1/10 is the same as 1/5 but right shifted by one place
#(and filling in the empty spot immediately after the decimal point with a zero).
echo "obase=2;ibase=10;1/10" | bc -l
.0001100110011001100110011001100110011001100110011001100110011001100

with the above information, give the binary representation of 1.6 ^[135]

Here is 1/25 in binary

echo "obase=2;ibase=10;1/25" | bc -l
.0000101000111101011100001010001111010111000010100011110101110000101

From this information, what is the binary representatin of 1/100 ^[136]

Just as 1/3 can't be represented by a finite number of decimal digits, 1/10 can't be represented by a finite number of binary digits. Any math done with 0.1 will be done with a 32-bit truncated representation of 0.1

>>> 0.1
0.10000000000000001
>>> 0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1
0.99999999999999989
>>> 0.1*10
1.0

The problem of not being able to represent finite decimal numbers in a finite number of binary digits is independant of the language. Here's an example with awk:

echo "0.1" | awk '{printf "%30.30lf\n", $1}'
0.100000000000000005551115123126

echo "0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1" | awk '{printf "%.30lf\n", $1+$2+$3+$4+$5+$6+$7+$8+$9+$10}'
0.999999999999999888977697537484

Do not test if two reals are equal. Even though the two numbers (to however many places you've displayed) appear the same, the computer may tell you that they're different. Instead you should test

abs(your_number - the_computers_number) < some_small_number

For the real way to do it see Lahey compiler.

Here's an example of how things don't work quite the way you'd expect.

>>> i=0.1
>>> if (i==0.1):	#is (i==0.1)?
...     print "true"
... 
true
>>> j=0
>>> for x in range(0,10):
...     j += i
... 
>>> j			#j should be 1.0, but you loose a 1 in the last place every time you add 0.1
0.99999999999999989
>>> print j		#outputs field width of 12 (and will round the number)
1.0
>>> print "%20.12f" %j	#print with explicit 12 digits after decimal point
      1.000000000000
>>> print "%20.20f" %j	#wider field
0.99999999999999988898
>>> print 1.0-j
1.11022302463e-16
>>> if (j==1.0):	#is (j==1.0)?
...     print "true"
... else:
...     print j
... 
1.0

Is (j==1.0) true? The answer is not yes or no; you aren't going to get a sensible answer. Knowing that, you should never ask such a question. In case you aren't convinced, let's see what might happen if you do.

(About 747s Airliner Takeoff Speeds, Boeing 747 http://www.aerospaceweb.org/aircraft/jetliner/b747/ Boeing 747-400 http://en.wikipedia.org/wiki/Boeing_747-400 http://www.aerospaceweb.org/question/performance/q0088.shtml). About diesel locomotives Electric Diesel Hauling II (http://www.cfr.ro/jf/engleza/0310/tehnic.htm) Steam Ranger Enthusiast Pages (http://www.steamranger.org.au/enthusiast/diesel.htm).

You've written the computer code to automatically load the Boeing 747-400ER cargo planes each night at the FedEx Memphis terminal. You have a terminal with 1500 palettes, each palette weighing 0.1Mg (about 200lbs). The max cargo payload is 139.7Mg.

It's 2am. All the packages have arrived by truck and are now sitting on palettes. Let's start loading cargo.

#! /usr/bin/python

palettes_in_terminal=[]	#make an empty list for the palettes in the terminal awaiting loading
palettes_in_747=[]	#make another empty list for the palettes loaded onto the plane
number_palettes=1500
weight_palette=0.1
weight_on_plane=0.0
max_weight_on_plane=139.7

#account for palettes in terminal
#make a list containing 1500 entries of 0.1
for i in range(0,number_palettes):
	palettes_in_terminal.append(weight_palette)
	

#load plane
#while plane isn't full and there are more palettes to load
#	take a palette out of the terminal and put it on the plane
while ((weight_on_plane != max_weight_on_plane) and (len(palettes_in_terminal) != 0)):
	#the next line is a train wreck version of this
	#moved_palette=palettes_in_terminal.pop()
	#palettes_in_747.append(moved_palette)
	palettes_in_747.append(palettes_in_terminal.pop())
	weight_on_plane += weight_palette
	#print "weight of cargo aboard %f" % weight_on_plane

print "weight on plane %f" % weight_on_plane
print "max weight on plane %f" % max_weight_on_plane
#-------------
	

What's this code doing? Swipe the code and run it. Is the plane safe to fly? How overloaded is it? How did the code allow the plane to become overloaded ^[137] ?

In an hour (at 3am), the plane, with a crew of 2, weighing 412,775 kg (about 400 tons, or 2-8 diesel locomotives), will be sitting at the end of the runway ready to take off, with its cargo and enough jet fuel (241,140l.) to make it across the country in time for the opening of the destination airport at 6am. (Why do the pilots have to wait till 6am, why couldn't they fly in earlier ^[138] ?) The pilot will spool up the engines, hold the plane for several seconds to check that the engines are running at full power, then let off the brakes, when the plane will start to roll. After thundering 3km down the runway, about a minute later alarms will alert the pilot that the apparently fully functional plane hasn't reached the lift off speed of 290 km/hr. The plane is too far down the runway to abort takeoff ^[139]. As far as the pilot knows, there is nothing wrong with the plane, only the speed is low. Is the indicated low speed an error and the the plane is really moving at the expected speed? Should the pilot rotate the plane and attempt lift off? He has only seconds to decide. Assuming the runway is long enough for the plane to eventually reach lift off speed, will it lift off ^[140] ? You'll read all about it in the papers next morning. In fact the pilot has no options and no decision to make. He was committed when he let the brakes off.

Why aren't there crash barriers at the end of the runway ^[141] ? There are better solutions for handling an overweight plane (see below).

The airline will blame the software company. The owners of the software business will protest that it was a problem with one of the computers that no-one could possibly have anticipated (there are people that will believe this). The american legal system will step in, the business will declare bankruptcy, the owners will have taken all their money out of the business long ago and have enough money to live very comfortably, the workers will be out of a job, and will find their pension fund unfinanced. The owners of the software business will be sued by the airline and the workers, but since the business is bankrupt, there is no money even if the suit is successful. Only the lawyers and the business owners will come out of this in good financial shape.

No-one would ever write such a piece of software. Even if you could equate reals, you wouldn't have written the code this way. Why not ^[142] ? Fix the code (you need to change the conditional statement). Here's my fixed version ^[143] .

While the algorithm I used here is completely stupid, the actual method that the FAA uses to calculate the take-off weight of a plane is more stupide (and I'm not making this up): the airline just makes up a value. They guess how much the passengers weigh and (from watching how my luggage is handled at check in) they also guess the weight of the baggage. The final decision is left to the pilots (at least in the case of US AirWays 5481 below), who have to decide by looking at the baggage and the passengers, whether it's safe to take off. This is the method that's used in the US. If you were a pilot, could you estimate the weight of passengers to 1% by looking out the cockpit door, down the aisles at the passengers? Pilots are trained to fly planes not to weigh passengers: scales are used to weigh planes.

Considering the consequences of attempting to take off overweight, it would be easy enough to weigh a plane before take-off, as is done for a truck or train: see Weigh Bridge (http://en.wikipedia.org/wiki/Weigh_bridge). Accuracy of current equipment is enough for the job: see Dynamass (www.pandrol.co.za/pdf/weigh_bridges.pdf) which can weigh a train moving at 35kph to 0.3% accuracy.

Planes attempt to take off overweight all the time.

The plane piloted by 7 yr old Jessica Dubroff, attempting to be the youngest girl to fly across the USA, crashed shortly after take off from Cheyenne (see Jessica Dubroff. http://en.wikipedia.org/wiki/Jessica_Dubroff). The plane was overloaded and attempted to take off in bad weather.

Most plane crashes due to overloading occur because the weight is not distributed correctly.

Air Midwest #5841 (http://en.wikipedia.org/wiki/US_Airways_Express_Flight_5481) out of Charlotte NC in Jan 2003 crashed on take off, because (among other things) the plane was overloaded by 600lbs, with the center of gravity 5% behind the allowable limit. The take-off weight was an estimate only, using the incorrect (but FAA approved) average passenger weight estimate, that hasn't been revised since 1936. The supersized passengers of the new millenium are porkers, weighing 20lbs more. The airline washed their hands of responsibility and left it to the pilots to decide whether to take off. Once in the air, the plane was tail heavy and the pilots couldn't get the nose down. The plane kept climbing till it stalled and crashed.

One would think that 32-bits is enough precision for a real, and in many cases (just adding or multiplying a couple of numbers) it is. However most of the time spent on computers is optimising multi-parameter models. Much scientific and engineering computing is devoted to modelling (making a mathematical representation for testing - weather, manufactured parts, bridges, electrical networks). You are often optimising a result with respect to a whole lot of parameters; e.g.

Optimisation is similar an ant's method for finding the top of a hill. All the ant knows is its position and it's altitude. It moves in some direction and takes note of whether it has gone uphill or downhill. When it can no longer move and gain altitude, the ant concludes that it is at the top of the hill and has finished its work. The area around the optimum is relatively flat and the ant may travel a long way in the x,y direction (or whatever the parameters are), before arriving at the optimum. Successful optimisation relies on the ant being able to discern a slope in the hill.

Because of the coarseness of floating point numbers, the hill instead of being smooth, is a series of slabs (with consecutive slabs of different thickness). An ant standing next to the edge of a slab, sees no change in altitude if it moves away from the edge, but if it had moved towards the edge would have seen a large change in altitude. If the precision of your computer's floating point calculations is too coarse, the computer will not find the optimum. In computerese - your computation will not converge to the correct answer and you won't be able to tell that you've got the wrong solution, or it will not converge at all - the ant will wander around a flat slab on the side of the hill, never realising that it's not at the top.

If the computation changes from 32 to 64-bit, how many slabs will now be in the interval originally covered by a 32-bit slab ^[144] ?

Because you can't rely on a 32-bit computation converging or getting the correct answer, scientists and engineers have been using 64-bit (or greater) computers for modelling and optimisation for the past 30yrs. You should not use 32 bit floating point for any work that involves repetitive calculation of small differences.

How do you know that your answer is correct and not an artefact of the low precision computations you're using? The only sure way of doing this is to go to the next highest precision and see if you get the same answer. This solution may require recoding the problem, or using hardware with more precision (which is likely unavailable, you'll already be using the most expensive computer you can afford). Programmers test their algorithm with test data for which they have known answers. If you make small changes in the data, you should get small changes in the answers from the computer. If the answers leap around, you know that the algorithm did not converge.

Money (e.g. $10.50) in a bank account looks like a real, but there is no such thing as 0.1c. Money needs to be represented accurately in a computer in multiples of 1c. For this computers use binary coded decimal (http://en.wikipedia.org/wiki/Binary-coded_decimal). This is an integer representation, based on 1c. You can learn about on this your own if you need it.

	Note
	End Lesson 19